原理:
1、采集阶段:对视频在时域上进行特殊的采样(不是传统的均匀完整采样),通过特定的采样策略和模式采集到远少于原始视频完整数据量的数据。
2、处理阶段:利用视频在时域上的相关性、稀疏性等特征以及数学算法等手段,对采集到的少量数据进行处理和分析。
3、恢复阶段:经过复杂的重构算法和运算等过程,从这些少量数据中恢复出原始视频或其近似视频(在一定的精度范围内)。
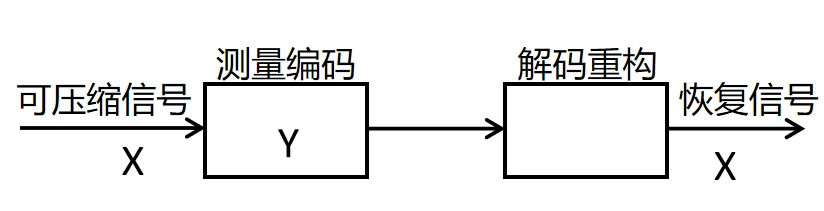
压缩感知,也被称为压缩采样,稀疏采样,压缩传感 。如果信号通过某种变换(小波变换、傅里叶变换等) 后,是稀疏的或者可压缩的, 则可以设计一个与变换基不相关的测量矩阵对原始信号进行测量,得到的测量信号通过求解非线性优化问题可实现信号的精确或近似重构。测量信号的维度远小于原始信号的维度,且测量信号只包含了信号的重要信息。压缩感知理论框架下图所示。
压缩感知理论将压缩与采样合并进行,以远低于奈奎斯特采样率的速率对信号进行非自适应的测量编码,突破了香农采样定理的瓶颈,使得高分辨率信号的采集成为可能。压缩感知的应用很大程度地减少了测量时间、采样速率及测量设备的数量。
压缩感知中,信号经过稀疏变换后,变换域信号可以看作是原始信号的一种简洁表达。信号能够稀疏表示是压缩感知理论的先验条件
稀疏的数学定义:信号X在正交基 下的变换系数向量为
,假如对于
和
,系数向量满足:
则说明该系数向量在某种意义上是稀疏的。如果变换系数的支撑域
的势不大于K,则称信号X是稀疏的,且稀疏度为K。
压缩感知理论应用的基础和前提是找到信号的最佳稀疏域。只有在合适的稀疏基下表示信号才能保证信号的稀疏度并使信号的稀疏度尽可能的小,不仅可以保证信号的恢复精度还能提高信号采集速度,有利于减少存储和传输信号所需资源。在研究信号的稀疏表示时,稀疏基的稀疏表示能力可以用排序后的变换系数的衰减速度来衡量。变换系数经过排序后满足幂次衰减并逐渐趋近于零,那么该信号称为可压缩信号,该信号可利用压缩感知技术进行编码重构,且重构误差满足:
其中,
是常数。
光滑信号经过傅里叶变换、小波变换后的信号以及具有不连续边缘的图像信号经过Curvelet变换后的信号都具有足够的稀疏性,因此可以利用压缩感知技术进行测量重构。
CS侦的编码过程:
对CS侦首先分成大小相等互不重叠的图像块,将每个图像块分别通过一定的规则(如按行,按列或者按ZigZag)扫描成一维信号,然后用随机测量矩阵对CS侦进行基于块的测量;最后将测量值按顺序直接传递到解码端,或者将测量值进行量化后按顺序传递到解码端。
CS侦的解码过程:
若编码端传送过来的是量化之后的信号,则在解码端相应的首先对接受信号进行反量化,然后再重构,否则直接进入重构步骤。为了提高重构视频侦的质量,利用重构关键帧或者相邻重构视频侦的对应位置宏块的邻域图像块构造字典,用该字典代替固定的稀疏基如离散余弦变换矩阵,由于时间相关性,视频信号具有更强的稀疏性,因此在测量值数目相同的条件下,CS侦具有更高的重构质量。但由于重构视频侦与原始视频侦之间存在一定的误差,在解码端的一个组内用重构CS侦为相邻后续视频侦构造字典进行稀疏重构,会产生误差传播现象。利用传统的分布式视频编码中的运动估计运动补偿技术或块预测技术生成边信息,该边信息可以看成是原始视频侦的一个估计,利用边信息辅助稀疏重构算法,可以加快重构算法的收敛速度以及视频信号重构质量。
信号重构算法是压缩感知理论的核心,是指由M个测量值重构长度为的稀疏信号或可压缩信号的过程。
1、基追踪算法
该算法采用最小1-范数在一定条件下和最小0-范数具有相同解的结论,用1-范数代替0-范数,得到以下式子:
考虑有噪声存在或允许一定的重构误差的情况下,上式可转换为:
其中,为重构误差。
匹配追踪算法的基本思路是通过迭代的方法从过完备库中搜索与信号最匹配的原子来逐步求解信号的稀疏解。该算法中每次迭代包含两步:原子选择和信号残差更新。原子选择是从过完备库中选择与当前残差最匹配的原子,相对应的投影长度用来衡量相关性;信号残差更新就是从残差中减去相关部分作为更新后的残差信号。
假设过完备库中的原子为,
,也就是投影矩阵中的第
个列向量为
,所有原子都经过了单位正则化,那么第j次迭代中的原子选择算法如下:
式中,表示内积,
表示第
次迭代后的残差,起始残差信号为原始信号,
表示与此次迭代所选取的最佳匹配原子相关的系数,记为
。然后算法按下式对残差信号进行更新:
若满足终止条件,如逼近残差小于期望的逼近误差限,则算法结束。
匹配追踪算法中,信号在已选定原子集合上的投影是非正交的,这使得每次迭代的结果可能是次最优的,因此可能需要经过较多次迭算法才能获得收敛,而且这种算法的逼近结果的稀疏性较差。
正交匹配追踪算法则有效克服了匹配追踪算法的缺点,该算法中的原子选择准则与匹配追踪算法相同,只是在迭代的每一步中都要对所选择的全部原子进行正交化处理以保证迭代的最优性,从而减少了迭代次数增加了收敛速度,提高了逼近信号的稀疏度。实验表明对固定K稀疏N维离散时间信号x,用一个的高斯矩阵测量时,只要
,正交匹配追踪算法就能以极大概率准确重构信号,而且比基追踪算法更快。
有先验知识辅助的正交匹配追踪算法是在OMP算法的基础上,解码器利用先验知识辅助进行信号的重构。解码器所获得的先验知识是根据已经重构信号的重要元素(非零大系数)的位置来估计当前信号重要元素的位置。这种对重要元素位置进行估计的先验知识不一定是完全正确的,可能存在一定的错误。所以在利用这些先验知识时要有一个纠正错误的机制。有先验知识辅助的正交匹配追踪算法在这些先验知识的辅助下,信号的重构过程比正常的正交匹配追踪算法快了许多。而有先验知识辅助的正交匹配追踪算法的信号重构恢复质量并不亚于正常的正交匹配追踪算法,计算复杂度却减小了很多。
对原始图像设定不同的压缩率或稀疏性,这两种算法完美或近似完美地重建图像的成功率都很高。匹配追踪法通常比较快,而基追踪算法在考虑到噪声时则显得比较准确。
BP和OMP算法都是基于信号在某一变换域具有稀疏性或可压缩性而进行的重构算法,而最小全变分法(Total Variation,TV)抛弃了这种思想,取而代之的是通过使特定的能量函数最小来实现信号重构,而且该算法是专门用于处理二维图像视频信号。具体的算法思想如下:
其中,x是二维图像信号,为Frobenius算子,ε>0为重构误差。假设
为二维离散信号,那么
表示一个二维图像信号的各像素点的梯度的幅值之和,该部分主要由噪声贡献,因此算法的基本思想就是在保证重构误差的条件下使恢复信号的噪声最小。该算法除了用于信号的重构,还特别适用于图像视频信号的去噪声和去模糊。
总之,目前为止压缩感知中出现的重构算法大致可分为以下三大类:
(1)凸松弛算法:为了找到信号的稀疏逼近,这类算法将非凸优化问题转化为凸优化问题来求解,如基追踪算法,梯度投影方法,内点法,和迭代阈值法。
(2)贪婪追踪算法:这类方法是通过迭代的方法逐步逼近原始信号的,在每次迭代时实现一个稀疏系数的求解。这类算法主要包括匹配追踪算法,OMP算法,分段OMP(StOMP)算法和正则化OMP(ROMP)算法等。
(3)组合算法:这类方法要求信号的采样支持通过分组测试快速重建,如傅立叶采样,链式追踪和HHS(HeavgHitters Oil Steroids)追踪等。
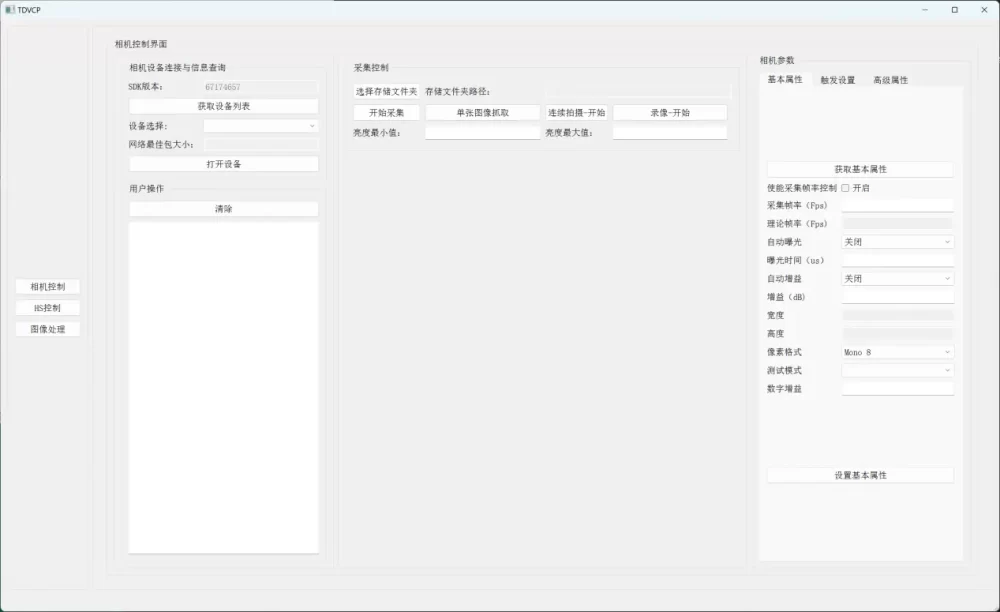
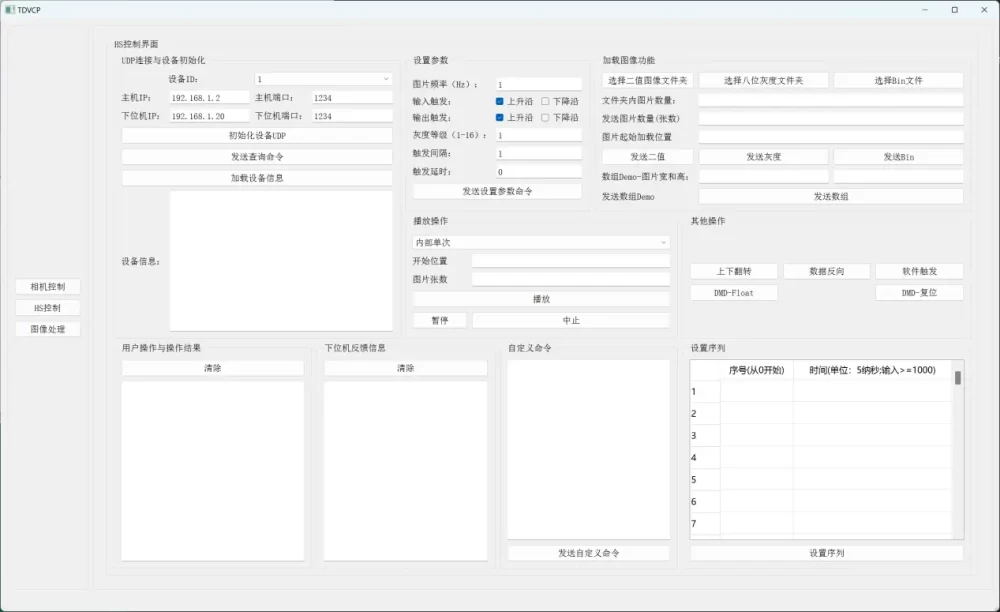
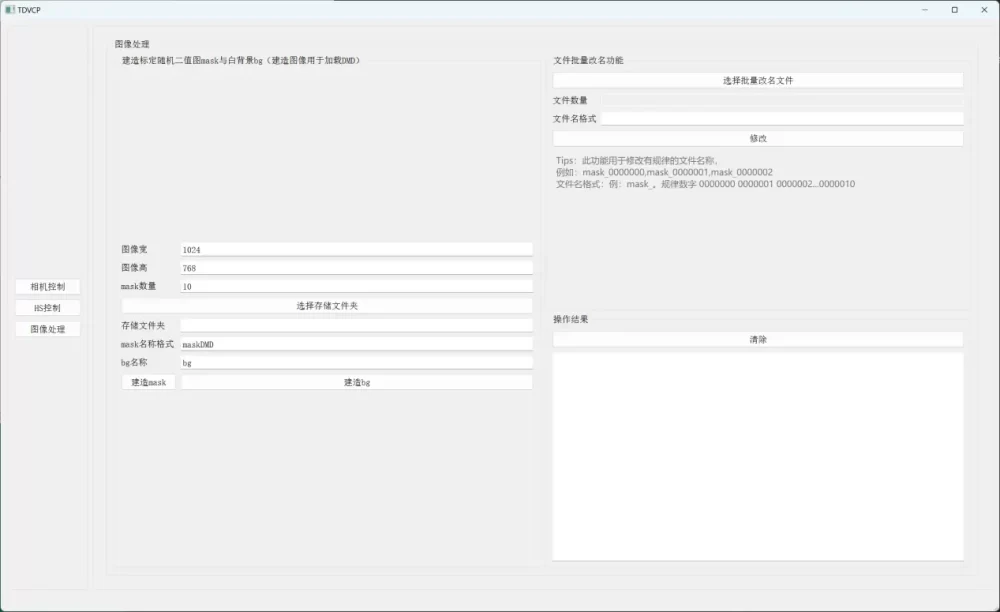
可视化软件操作界面,软件上集成模组驱动控制,使用便捷。
测试效果:
主要硬件清单
| 名称 | 规格型号 | 单位 | 数量 |
| 超高速数字微镜空见光调制器 | F4320 DDR 0.7XGA | 套 | 1 |
| 面阵相机 | 320万像素 | 个 | 1 |
| 远心镜头 | 放大倍率0.5 | 个 | 1 |
| 远心镜头 | 放大倍率1 | 个 | 1 |
| 定焦镜头 | 25mm焦距1000万像素 | 个 | 1 |
| TIR棱镜 | K9 | 个 | 1 |
| 支架 | 含底板、接杆、杆架、叉块、螺纹转接件、微调平台、底座、反射镜支架、M6螺钉(若干) | 套 | 1 |
| 工具 | 面包板把手 | 套 | 1 |
| LED灯 | 120W | 个 | 1 |
相比传统视频压缩技术在特定场景下可能具有更高的压缩比;可以一定程度上缓解传统视频处理中时空分辨率相互制约等矛盾;对于一些资源受限(如存储容量有限、传输带宽有限等)的应用场景具有重要意义。